|
Distinguished Author Series VIRTUAL INTELLIGENCE
AND ITS APPLICATIONS IN PETROLEUM ENGINEERING 1. Artificial Neural
Networks Shahab Mohaghegh This
is the first of a three-article series on Virtual Intelligence and its applications
in petroleum and natural gas engineering. In addition to discussing artificial
neural networks, the series will include articles on evolutionary programming
and fuzzy logic. Intelligent hybrid systems that incorporate an integration of
two or more of these paradigms and their application in the oil and gas
industry will also be discussed in these articles. The intended audience is the
petroleum professional that is not quite familiar with virtual intelligence but
would like to know more about this technology and its potentials. Those with a
prior understanding and experience of the technology will also find the
articles useful and informative. Definitions and
Background In
this section some historical background of the technology will be mentioned
followed by definitions of virtual intelligence and artificial neural networks.
After the definitions, more general information on the nature and mechanism of
the artificial neural network and its relevance to biological neural networks
will be offered. Virtual
intelligence has been called by different names. It has been referred to as
"artificial intelligence", "computational intelligence" and
"soft computing." There seems not to be a uniformly acceptable name
for this collection of analytic tools among the researchers and practitioners
of the technology. Among these names "artificial intelligence" is
used the least as an umbrella term. This is due to the fact that
"artificial intelligence" has been historically referred to
rule-based expert systems and today is used synonymously with expert systems.
Expert systems made many promises of delivering intelligent computers and
programs, but these promises never materialized. Many believe that term
"soft computing" is the most appropriate term to be used and
"virtual intelligence" is a subset of "soft
computing". Although there is
merit to this argument we will continue using the term "virtual
intelligence" throughout these articles. Virtual
intelligence may be defined as a collection of new analytic tools that attempts
to imitate life1. Virtual intelligence techniques exhibit an ability
to learn and deal with new situations. Artificial neural networks, evolutionary
programming and fuzzy logic are among the paradigms that are classified as
virtual intelligence. These techniques possess one or more attributes of
"reason", such as generalization, discovery, association and
abstraction2. In the last
decade virtual intelligence has matured to a set of analytic tools that
facilitate solving problems that were previously difficult or impossible to
solve. The trend now seems to be the integration of these tools together, as
well as with conventional tools such as statistical analysis, to build
sophisticated systems that can solve challenging problems. These tools are now
used in many different disciplines and have found their way into commercial
products. Virtual intelligence is used in areas such as medical diagnosis,
credit card fraud detection, bank loan approval, smart household appliances,
subway systems, automatic transmissions, financial portfolio management, robot
navigation systems, and many more. In the oil and gas industry these tools have
been used to solve problems related to pressure transient analysis, well log
interpretation, reservoir characterization, and candidate well selection for
stimulation, among other things. A Short History of
Neural Networks Neural
network research can be traced back to a paper by McCulloch and Pitts3
in 1943. In 1957 Frank Rosenblatt invented the Perceptron4.
Rosenblatt proved that given linearly separable classes, a peceptron would, in
a finite number of training trials, develop a weight vector that will separate
the classes (a pattern classification task). He also showed that his proof
holds independent of the starting value of the weights. Around the same time
Widrow and Hoff5 developed a similar network called Adeline. Minskey
and Papert6 in a book called "Perceptrons" pointed out
that the theorem obviously applies to those problems that the structure is
capable of computing. They showed that elementary calculation such as simple
"exclusive or" (XOR) problems cannot be solved by single layer
perceptrons. Rosenblatt4
had also studied structures with more layers and believed that they could
overcome the limitations of simple perceptrons. However, there was no learning
algorithm known which could determine the weights necessary to implement a
given calculation. Minskey and Papert doubted that one could be
found and recommended that other approaches to artificial intelligence should
be pursued. Following this discussion, most of the computer science community
left the neural network paradigm for twenty years7. In early 1980s
Hopfield was able to revive the neural network research. Hopfield’s efforts coincided with
development of new learning algorithms such as backpropagation. The growth of
neural network research and applications has been phenomenal since this
revival. Structure of a
Neural Network An
artificial neural network is an information processing system that has certain
performance characteristics in common with biological neural networks.
Therefore it is appropriate to describe briefly a biological neural network
before offering a detail definition of artificial neural networks. All living organisms are made up of cells.
The basic building blocks of the nervous system are nerve cells, called
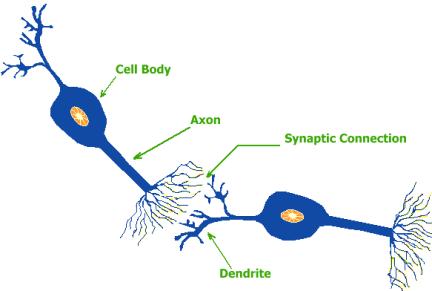
neurons. Figure 1 shows a schematic diagram of two bipolar neurons.
Figure 1. Schematic diagram of two bipolar
neurons. A typical neuron contains a cell body where the nucleus is located, dendrites and an axon. Information in the form of a train of electro-chemical pulses (signals) enters the cell body from the dendrites. Based on the nature of this input the neuron will activate in an excitatory or inhibitory fashion and provides an output that will travel through the axon and connects to other neurons where it becomes the input to the receiving neuron. The point between two neurons in a neural pathway, where the termination of the axon of one neuron comes into close proximity with the cell body or dendrites of another, is called a synapse. The signals traveling from the first neuron initiate a train of electro-chemical pulse (signals) in the second neuron. It
is estimated that the human brain contains on the order of 10 to 500 billion
neurons8. These neurons are divided into modules and each module
contains about 500 neural networks9. Each network may contain about
100,000 neurons in which each neuron is connected to hundreds to thousands of
other neurons. This architecture is the main driving force behind the complex
behavior that comes so natural to us. Simple tasks such as catching a ball,
drinking a glass of water or walking in a crowded market require so many
complex and coordinated calculations that sophisticated computers are unable to
undertake the task, and yet is done routinely by humans without a moment of
thought. This becomes even more
interesting when one realizes that neurons in the human brain have cycle time
of about 10 to 100 milliseconds while the cycle time of a typical desktop
computer chip is measured in nanoseconds. The human brain, although million
times slower than common desktop PCs, can perform many tasks orders of
magnitude faster than computers because of it massively parallel architecture. Artificial
neural networks are a rough approximation and simplified simulation of the
process explained above. An artificial neural network can be defined as an
information processing system that has certain performance characteristics
similar to biological neural networks. They have been developed as
generalization of mathematical models of human cognition or neural biology,
based on the assumptions that: 1.
Information
processing occurs in many simple elements that are called neurons (processing
elements). 2.
Signals are passed
between neurons over connection links. 3.
Each connection link
has an associated weight, which, in a typical neural network, multiplies the
signal being transmitted. 4.
Each neuron applies
an activation function (usually non-linear) to its net input to determine its
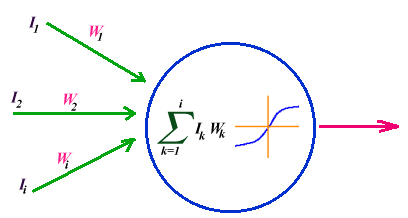
output signal10. Figure
2 is a schematic diagram of a typical neuron (processing element) in an
artificial neural network. Output from other neurons is multiplied by the
weight of the connection and enters the neuron as input. Therefore an artificial
neuron has many inputs and only one output. The inputs are summed and
subsequently applied to the activation function and the result is the output of
the neuron.
Figure 2. Schematic diagram of an artificial
neuron or a processing element. Mechanics of Neural
Networks Operation An
artificial neural network is a collection of neurons that are arranged in
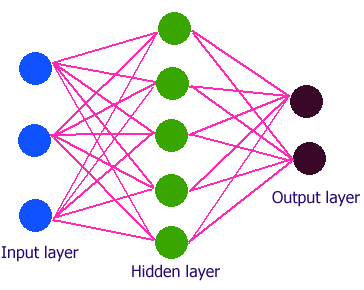
specific formations. Neurons are grouped into layers. In a multi-layer network
there are usually an input layer, one or more hidden layers and an output
layer. The number of neurons in the input layer corresponds to the number of
parameters that are being presented to the network as input. The same is true
for the output layer. It should be
noted that neural network analysis is not limited to a single output and that
neural nets can be trained to build neuro-models with multiple outputs. The
neurons in the hidden layer or layers are mainly responsible for feature
extraction. They provide increased dimensionality and accommodate tasks such as
classification and pattern recognition. Figure 3 is a schematic diagram of a
fully connected three layered neural network. There
are many kinds of neural networks. Neural network scientists and practitioners
have provided different classifications for neural networks. One of the most
popular classifications is based on the training methods. Neural nets can be divided into two major
categories based on the training methods, namely supervised and unsupervised
neural networks. Unsupervised neural networks, also known as self-organizing
maps, are mainly clustering and classification algorithms. They have been used
in oil and gas industry to interpret well logs and to identify lithology. They
are called unsupervised simply because no feedback is provided to the network.
The network is asked to classify the input vectors into groups and clusters.
This requires a certain degree of redundancy in the input data and hence the
notion that redundancy is knowledge11.
Figure 3. Schematic diagram of a three-layer
neuron network. Most
of the neural network applications in the oil and gas industry are based on
supervised training algorithms. During a supervised training process both input
and output are presented to the network to permit learning on a feedback basis.
A specific architecture, topology and training algorithm is selected and the
network is trained until it converges.
During the training process neural network tries to converge to an
internal representation of the system behavior. Although by definition neural
nets are model-free function approximators, some people choose to call the
trained network a neuro-model. The
connections correspond roughly to the axons and synapses in a biological
system, and they provide a signal transmission pathway between the nodes. Several layers can be interconnected. The
layer that receives the inputs is called the input layer. It typically performs
no function other than the buffering of the input signal. The network outputs
are generated from the output layer. Any other layers are called hidden layers because they are internal to the network and have no direct
contact with the external environment. Sometimes they are likened to a
"black box" within the network system. However, just because they are
not immediately visible does not mean that one cannot examine the function of
those layers. There may be zero to several hidden layers. In a fully connected
network every output from one layer is passed along to every node in the next
layer. In
a typical neural data processing procedure, the database is divided into three
separate portions called training, calibration and verification sets. The training set is used to develop the
desired network. In this process (depending on the paradigm that is being
used), the desired output in the training set is used to help the network
adjust the weights between its neurons or processing elements. During the
training process the question arises as when to stop the training. How many
times should the network go through the data in the training set in order to
learn the system behavior? When should the training stop? These are legitimate
questions, since a network can be over trained. In the neural network related
literature over-training is also referred to as memorization. Once the network memorizes
a data set, it would be incapable of generalization. It will fit the training
data set quite accurately, but suffers in generalization. Performance of an
over-trained neural network is similar to a complex non-linear regression
analysis. Over-training
does not apply to some neural network paradigms simply because they are not
trained using an iterative process. Memorization and over-training is
applicable to those networks that are historically among the most popular ones
for engineering problem solving. These include back-propagation networks that
use an iterative process during the training. In
order to avoid over training or memorization, it is a common practice to stop
the training process every so often and apply the network to the calibration
data set. Since the output of the
calibration data set is not presented to the network, one can evaluate
network's generalization capabilities by how well it predicts the calibration
set's output. Once the training process is completed successfully, the network
is applied to the verification data set.
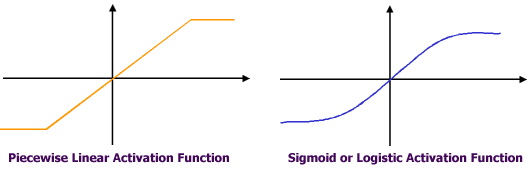
Figure 4. Commonly used activation functions in
artificial neurons.
During the training process each
artificial neuron (processing element) handles several basic functions. First,
it evaluates input signals and determines the strength of each one. Second, it
calculates a total for the combined input signals and compares that total to
some threshold level. Finally, it determines what the output should be. The
transformation of the input to output -
within a neuron - takes place using an activation function. Figure 4 shows two
of the commonly used activation (transfer) functions. All
the inputs come into a processing element simultaneously. In response, neuron
either "fires" or "doesn't fire," depending on some
threshold level. The neuron will be
allowed a single output signal, just as in a biological neuron - many inputs,
one output. In addition, just as things
other than inputs affect real neurons, some networks provide a mechanism for
other influences. Sometimes this extra input is called a bias term, or a forcing term. It could also be a forgetting term, when a system needs to
unlearn something12. Initially
each input is assigned a random relative weight (in some advanced applications
– based on the experience of the practitioner- the relative weight assigned
initially may not be random). During the training process the weight of the
inputs is adjusted. The weight of the input represents the strength of its
connection to the neuron in the next layer. The weight of the connection will
affect the impact and the influence of that input. This is similar to the
varying synaptic strengths of biological neurons. Some inputs are more important than others in the way they
combine to produce an impulse. Weights are adaptive coefficients within the
network that determine the intensity of the input signal. The initial weight
for a processing element could be modified in response to various inputs and
according to the network's own rules for modification. Mathematically, we
could look at the inputs and the weights on the inputs as vectors, such as II, I2 . . . In
for inputs and Wl, W2
. . . Wn for weights. The total input signal is the dot, or
inner, product of the two vectors. Geometrically, the inner product of two
vectors can be considered a measure of their similarity. The inner product is
at its maximum if the vectors point in the same direction. If the vectors point
in opposite directions (180 degrees), their inner product is at its minimum.
Signals coming into a neuron can be positive (excitatory) or negative
(inhibitory). A positive input promotes the firing of the processing element,
whereas a negative input tends to keep the processing element from firing.
During the training process some local memory can be attached to the processing
element to store the results (weights) of previous computations. Training is
accomplished by modification of the weights on a continuous basis until
convergence is reached. The ability to change the weights allows the network to
modify its behavior in response to its inputs, or to learn. For example, suppose a network identifies a production well as
"an injection well." On successive iterations (training), connection
weights that respond correctly to a production well are strengthened and those
that respond to others, such as an injection well, are weakened until they fall
below the threshold level and the correct recognition of the well is achieved. In the back
propagation algorithm (one of the most commonly used supervised training
algorithms) the network output is compared with the desired output - which is
part of the training data set, and the difference (error) is propagated
backward through the network. During
this back propagation of error the weights of the connections between neurons
are adjusted. This process is continued in an iterative manner. The network
converges when its output is within acceptable proximity of the desired
output. Applications in the Oil and Gas Industry Common sense
indicates that if a problem can be solved using conventional methods, one
should not use neural networks or any other virtual intelligence technique to
solve them. For example, balancing your checkbook using a neural network is not
recommended. Although there is academic
value to solving simple problems, such as polynomials and differential
equations, using neural networks to show its capabilities, they should be used
mainly in solving problems that otherwise are very time consuming or simply
impossible to solve by conventional methods. Neural networks have
shown great potential for generating accurate analysis and results from large
historical databases. The kind of data
that engineers may not consider valuable or relevant in conventional modeling
and analysis processes. Neural networks should be used in cases where
mathematical modeling is not a practical option. This may be due to the fact
that all the parameters involved in a particular process are not known and/or
the inter-relation of the parameters is too complicated for mathematical
modeling of the system. In such cases a neural network can be constructed to
observe the system behavior (what types of output is produced as a result of
certain set of inputs) and try to mimic its functionality and behavior. In this
section few examples of applying artificial neural networks to petroleum
engineering related problems is presented. Reservoir
Characterization Neural
networks have been utilized to predict or virtually measure formation
characteristics such as porosity, permeability and fluid saturation from
conventional well logs13-15. Using well logs as input data coupled
with core analysis of the corresponding depth, these reservoir characteristics
were successfully predicted for a heterogeneous formation in West Virginia. There
have been many attempts to correlate permeability with core porosity and/or
well logs using mathematical or statistical functions since the early 1960s16.
It was shown that a carefully orchestrated neural network analysis is capable
of providing more accurate and repeatable results when compared to methods used
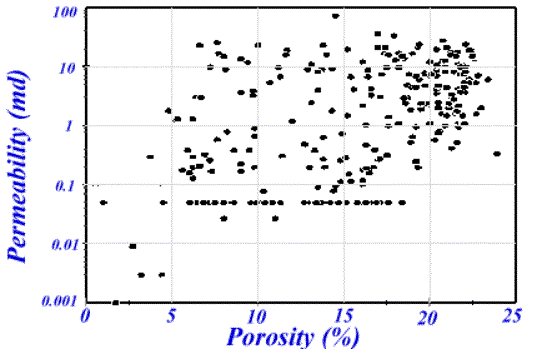
previously17. Figure 5 is a
cross-plot of porosity versus permeability for the “Big Injun” formation in
West Virginia. It is obvious that there are no apparent correlation between
porosity and permeability in this formation.
The scatter of this plot is mainly due to the complex and heterogeneous
nature of this reservoir.
Figure 5. Porosity and permeability cross-plot
for Big Injune formation. Well logs provide a
wealth of information about the rock, but they fall short in measurement and
calculation of its permeability. Dependencies of rock permeability on
parameters that can be measured by well logs have remained one of the
fundamental research areas in petroleum engineering. Using the conventional
computing tools available, scientists have not been able to prove that a
certain functional relationship exists that can explain the relationships in a
rigorous and universal manner. Author suggest that if such dependency or
functional relation exists, an artificial neural network is the tool to find
it. Using
geophysical well log data as input (bulk density, gamma ray, and induction
logs), a neural network was trained to predict formation permeability measured
from laboratory core analyses. Log and core permeability data were available
from four wells. The network was trained with the data from three wells and
attempted to predict the measurements from the fourth well. This practice was repeated twice each time
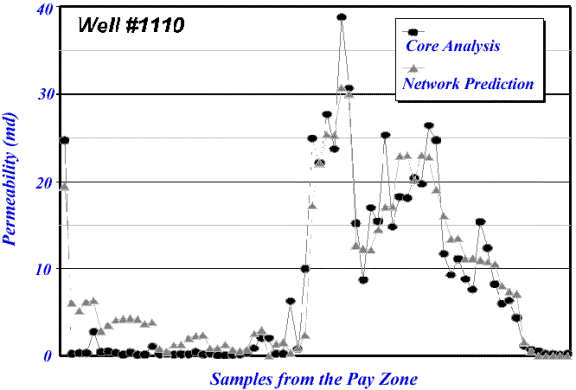
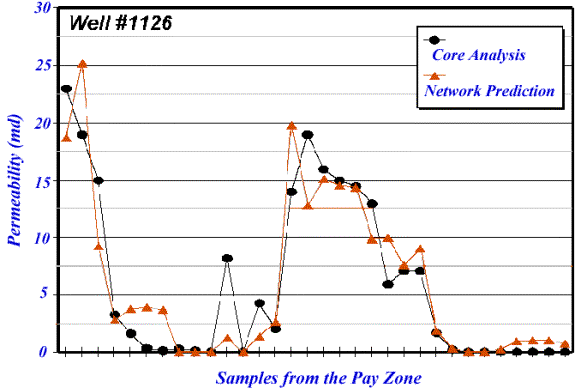
using a different well as the verification well. Figures 6 and 7 show the
result of neural network’s prediction compared to the actual laboratory
measurements. Please note that the well logs and core measurements from these
test wells were not used during the training process. In
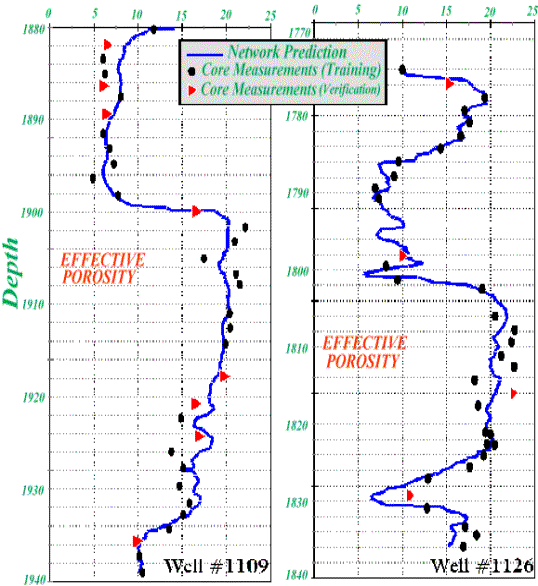
a similar process well logs were used to predict (virtually measure) effective
porosity and fluid saturation in this formation. The results of this study are
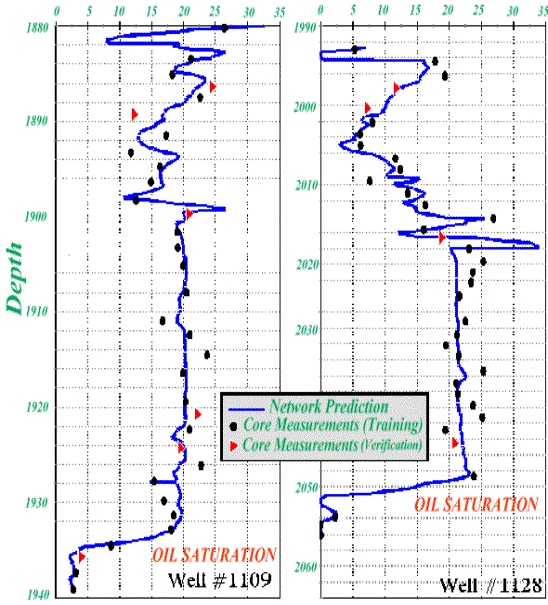
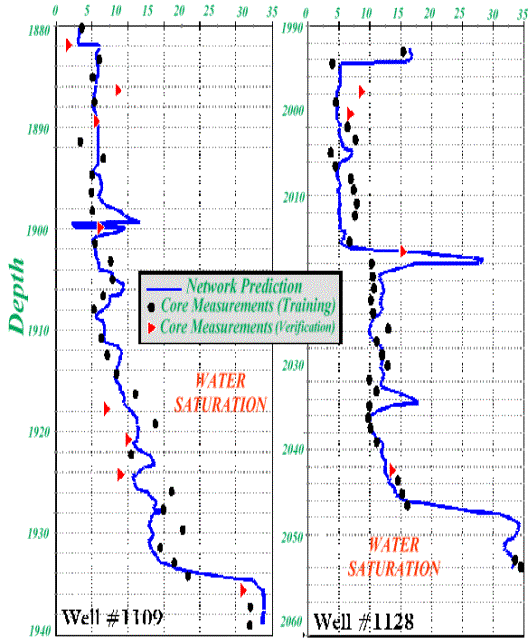
shown in Figures 8 through 10. In these figures solid lines show the neural
network’s predictions. The core measurements are shown using two different
symbols. The circles are those core measurements that were used during the
training process and the triangles are the core measurements that were never
seen by the network.
Figure 6. Core and network permeability for well
1110 in Big Injun formation.
Figure 7. Core and network permeability for well
1126 in Big Injun formation.
Figure 8. Core and network effective porosity
for well 1109 and 1126 in Big Injun formation.
Figure 9. Core and network oil saturation for
well 1109 and 1128 in Big Injun formation.
Figure 10. Core and network water saturation for
well 1109 and 1128 in Big Injun formation. Virtual Magnetic
Resonance Imaging Logs
Figure 11. Using virtual MRI log methodology in a
typical field. Table
1 shows the accuracy of this methodology when applied to the four wells being
studied. For each well the methodology was applied to three different MRI logs
namely MPHI (effective porosity), MBVI (irreducible water saturation), and
MPERM (permeability). For each log the table shows the correlation coefficient
both for the entire well data set (training data and verification data) and for
only the verification data set. The verification data set includes data that
had not been seen previously by the network. The correlation coefficient of
this methodology ranges from 0.80 to 0.97. As expected, the correlation
coefficient for the entire well data set is better than that of the
verification data set. This is due to the fact that the training data set is
included in the entire well data set and that correlation coefficient for the
training data is usually higher than the verification data set.
Table 1. Results of virtual MRI logs for four
wells in the United States. MRI
logs are also used to provide a more realistic estimate of recoverable reserve
as compared to conventional well logs. Table 2 shows the recoverable reserve
calculated using actual and virtual MRI logs. Recoverable reserve calculations
based on virtual MRI logs are quite close to those of actual MRI logs since
during the reserve calculation a certain degree of averaging takes place that
compensates for some of the inaccuracies that are associated with virtual MRI
logs. As shown in Table 2 in all four cases the recoverable reserve calculated
using Virtual MRI logs are within 2% of those calculated using actual MRI logs.
In the case of the well in the Gulf of Mexico the percent difference is about
0.3%. Although there is not enough evidence to make definitive conclusions at
this point, but it seems that recoverable reserve calculated using virtual MRI
logs are mostly on the conservative sides.
Table 2. Recoverable reserve calculations using
actual and virtual MRI logs. Figures
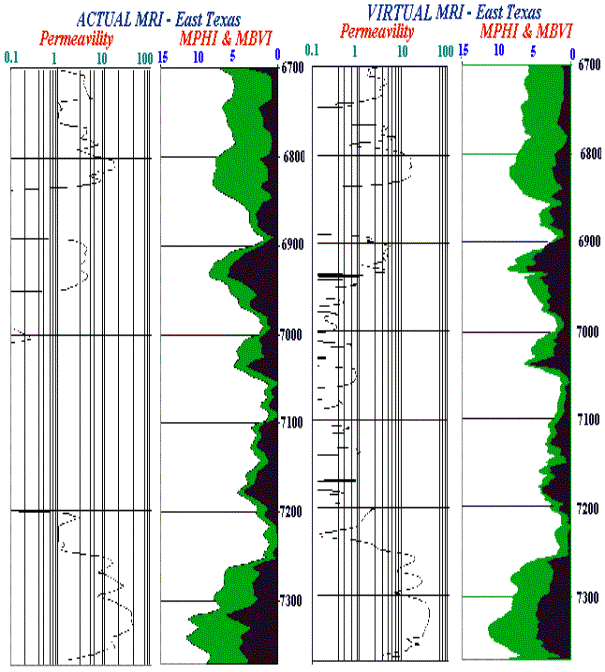
12 and 13 show the comparison between actual and virtual MRI logs for the well
located in East Texas.
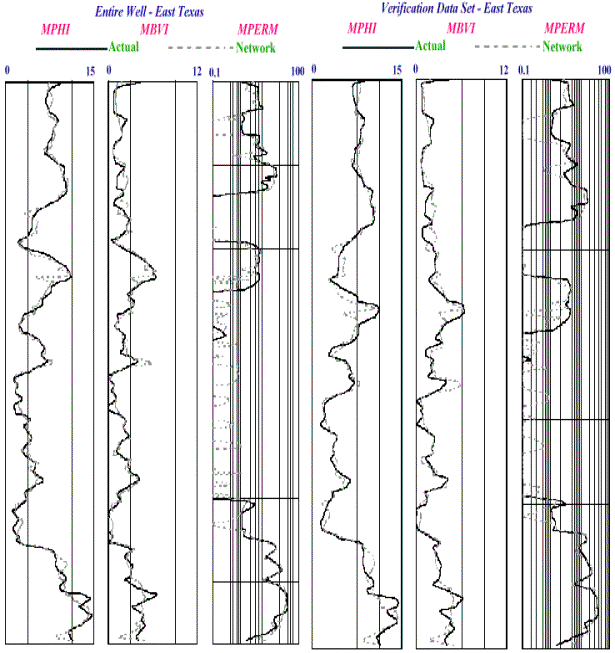
Figure 12. Virtual MRI log results for the well
in East Texas, for verification data set and the entire well data set.
Figure 13. Actual and Virtual MRI log results for
the well in East Texas. There
are many more applications of neural networks in the oil and gas industry. They
include application to field development19, two-phase flow in pipes20-21,
identification of well test interpretation models22-24, completion
analysis25-26, formation damage prediction27,
permeability prediction28-29, and fractured reservoirs30-31.
Closing RemarksAuthor Alvin Toeffler
has been quoted to say, “The responsibility for change … lies within us. We must begin with ourselves, teaching
ourselves not to close our minds prematurely to the novel, the surprising, and
the seemingly radical.” Virtual
intelligence in general and artificial neural networks specifically has
advanced substantially in the past decade. There are many everyday applications
and products that use these tools to make life easier for human kind. Petroleum
engineers historically have been among the most open-minded scientists and
practitioners that have embraced new technology and turned it to the task of
problem solving. Neural network seems to be one of the newest tools that is
finding its way into the oil and gas industry as an alternative analytical
method. This technology is in its infancy and has great
potential. Most of neural network application of today is conducted in the
software domain. Hardware implementations have already started becoming more
and more popular. The integration of neural networks with fuzzy logic and
genetic programming techniques (that will be covered in the next articles) is
providing ever more powerful tools. A word of caution seems to be appropriate at this time.
It has been the observation of this author – which seems to be shared by other
neural network practitioners in our field - that successful application of
neural networks to complex and challenging problems is directly related to the
experience one will gain by working with this tool and its many variations.
Therefore, failure of early attempts to solve complex problems should not cause
the user to despair of the technology.
Of course, even novice users of the technology can achieve good results
when solving straightforward problems using neural networks. References 1.
Zaruda, J. M. Marks,
R. J., Robinson, C. J. Computational
Intelligence, Imitating Life, IEEE Press, Piscataway, NJ, 1994. 2.
Eberhart, R.,
Simpson, P., Dobbins, R. Computational
Intelligence PC Tools, Academic Press, Orlando, FL, 1996. 3.
McCulloch, W. S.,
and Pitts, W. "A Logical Calculus of Ideas Immanent in Nervous
Activity," Bulletin of Mathematical Biophysics, 5, pp. 115 - 133, 1943. 4.
Rosenblatt, F.
"The Perceptron: Probabilistic Model for Information Storage and
Organization in the Brain," Psychol. Rev. 65, pp. 386-408, 1958. 5.
Widrow, B.
"Generalization and Information Storage in Networks of Adeline
Neurons," Self-Organizing Systems,
Yovitz, M.C., Jacobi, G. T., and Goldstein, G. D. editors, pp. 435 - 461,
Chicago, 1962. 6.
Minsky, M. L. and
Papert, S. A. Perceptrons, MIT Press,
Cambridge, MA, 1969. 7.
Hertz, J., Krogh,
A., Palmer, R. G. Introduction to the
Theory of Neural Computation, Addison-Wesley Publishing Company, Redwood
City, CA, 1991. 8.
Rumelhart, D. E.,
and McClelland, J. L. Parallel
Distributed processing, Exploration in the Microstructure of Cognition, Vol. 1:
Foundations, MIT Press, Cambridge, MA, 1986. 9.
Stubbs, D.
Neurocomputers. M. D. Computing,
5(3): 14-24, 1988. 10.
Fausett, L. Fundamentals of Neural Networks,
Architectures, Algorithms, and Applications, Prentice Hall, Englewood
Cliffs, NJ, 1994. 11.
Barlow, H. B.
Unsupervised learning. Neural Computation 1, 295-311, 1988. 12.
McCord Nelson, M.,
and Illingworth, W.T. A Practical Guide
to Neural Nets, Addison-Wesley Publishing, Reading, MA 1990. 13.
Mohaghegh, S.,
Arefi, R., Bilgesu, I., Ameri, S. "Design and Development of an Artificial
Neural Network for Estimation of Formation Permeability," SPE Computer
Applications, December 1995, pp. 151-154. 14.
Mohaghegh, S.,
Arefi, R., Ameri, S. "Petroleum Reservoir Characterization with the Aid of
Artificial Neural Networks," Journal of Petroleum Science and Engineering,
16, 1996, pp. 263-274. 15.
Mohaghegh, S.,
Ameri, S., and Arefi, R. "Virtual Measurement of Heterogeneous Formation
Permeability Using Geophysical Well Log Responses," The Log Analyst,
March/April 1996, pp. 32-39. 16.
Balan, B.,
Mohaghegh, S., and Ameri, S. "State-of-the-art in Permeability
Determination From Well Log Data: Part 1: A Comparative Study, Model
Development," SPE 30978, Proceedings, SPE Easter Regional Conference Sept.
17-21, 1995, Morgantown, WV. 17.
Mohaghegh, S.,
Balan, B., and Ameri, S. "State-of-the-art in Permeability Determination
From Well Log Data: Part 2: Verifiable, Accurate Permeability Prediction, the
Touch-Stone of All Models," SPE 30979, Proceedings, SPE Easter Regional
Conference Sept. 17-21, 1995, Morgantown, WV. 18.
Mohaghegh, S.,
Richardson, M., and Ameri, M. “Virtual Magnetic Resonance Imaging Logs:
Generation of Synthetic MRI Logs From Conventional Well Logs,” SPE 51075,
Proceedings, SPE Eastern Regional Conference Nov. 9-11, 1998, Pittsburgh, PA. 19.
Doraisamy, H.,
Ertekin, T., Grader, A. "Key Parameters Controlling the Performance of
Neuro Simulation Applications in Field Development," SPE 51079,
Proceedings, SPE Eastern Regional Conference Nov. 9-11, 1998, Pittsburgh, PA. 20.
Ternyik, J.,
Bilgesu, I., and Mohaghegh, S. " Virtual
Measurement in Pipes, Part 2: Liquid Holdup and Flow Pattern Correlation," SPE 30976, Proceedings, SPE Eastern
Regional Conference and Exhibition, September 19-21, 1995, Morgantown, West
Virginia 21.
Ternyik, J.,
Bilgesu, I., Mohaghegh, S., and Rose, D., "Virtual Measurement in Pipes,
Part 1: Flowing Bottomhole Pressure Under Multi-phase Flow and Inclined
Wellbore Conditions," SPE 30975, Proceedings,
SPE Eastern Regional Conference and Exhibition, September 19-21, 1995,
Morgantown, West Virginia. 22.
Sung, W., Hanyang,
U., Yoo, I. "Development of HT-BP Neural Network System for the
Identification of Well Test Interpretation Model," SPE 30974, Proceedings, SPE Eastern Regional
Conference and Exhibition, September 19-21, 1995, Morgantown, West Virginia. 23.
Al‑Kaabi, A.,
Lee, W. J., "Using Artificial Neural Nets to Identify the Well Test
Interpretation Model," SPE Formation Evaluation, Sept. 1993, pp. 233-240 24.
Juniardi, I. J.,
Ershaghi, I., "Complexities of Using Neural Networks In Well Test Analysis
of Faulted Reservoir," SPE 26106, Proceedings, SPE Western Regional
Meeting, 26‑28 March 1993, Anchorage, Alaska. 25.
Shelley, R.,
Massengill, D., Scheuerman, P., McRill, P., Hamilton, R. "Granite Wash
Completion Optimization with the Aid of Artificial Neural Networks," SPE
39814, Proceedings, Gas Technology Symposium, March 15-18, 1998, Calgary,
Alberta. 26.
Shelley, R., Stephenson,
S., Haley, W., Craig, E. "Red Fork Completion Analysis with the Aid of
Artificial Neural Networks," SPE 39963, Proceedings, Rocky Mountain
Regional Meeting / Low Permeability Reservoir Symposium, April 5-8, 1998,
Denver, CO. 27.
Nikravesh, M., Kovscek,
A. R., Jonston, R. M., and Patsek, T. W. "Prediction of Formation Damage
During the Fluid Injection into Fractured Low Permeability Reservoirs via
Neural networks," SPE 31103, Proceedings, SPE Formation Damage Symposium,
Feb. 16-18, 1996, Lafayette, LA. 28.
Wong, P. M.,
Taggart, I. J., Jian, F. X. "A Critical Comparison of Neural networks and
Discriminant Analysis in Lithofacies, Porosity and Permeability
Predictions," Journal of Petroleum Geology, 18 (2), pp. 191-206, 1995. 29.
Wong, P. M.,
Henderson, D. J., Brooks, L. J. "Permeability Determination using Neural
Networks in the Ravva Field, Offshore India," SPE reservoir Evaluation and
Engineering 1 (2), pp. 99-104, 1998. 30.
Ouense, A., Zellou, A., Basinski, P. M., and
Head, C. F. "Use of Neural Networks in Tight Gas Fractured Reservoirs:
Application to San Juan Basin," SPE 39965, Proceedings, Rocky Mountain
Regional Meeting / Low Permeability Reservoir Symposium, April 5-8, 1998,
Denver, CO. 31.
Zellou, A., Ouense,
A., and Banik, A. "Improved Naturally Fractured Reservoir Characterization
Using Neural networks, Geomechanics and 3-D Seismic," SPE 30722,
Proceedings, SPE Annual Technical Conference and Exhibition, October 22-25,
1995, Dallas, TX. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||