|
Distinguished Author Series VIRTUAL
INTELLIGENCE AND ITS APPLICATIONS IN PETROLEUM ENGINEERING Part
2. Evolutionary Computing Shahab
Mohaghegh In part one of this series, artificial neural networks were discussed, and a general definition of virtual intelligence was provided. The goal of this article is to provide an overview of evolutionary computing, its potential combination with neural networks to produce powerful intelligent applications, and its applications in the oil and gas industry. The most successful intelligent applications incorporate several virtual intelligence tools in a hybrid manner. Virtual intelligence tools complement each other and are able to amplify each other’s effectiveness. In this article, a general overview of evolutionary computation and its background – as related to the Darwinian evolution theory - is presented. This is followed by a more detailed look at genetic algorithms as the primary evolutionary computing paradigm that is mostly used. The article will continue and conclude by exploring the application of a hybrid neural network/genetic algorithm system to a petroleum engineering related problem. BACKGROUND
Evolutionary computing, like other
virtual intelligence tools, has its roots in nature. It is an attempt to mimic
the evolutionary process using computer algorithms and instructions. However,
why would we want to mimic the evolution process? The answer will become
obvious once we realize what type of problems the evolution process solves and
whether we would like to solve similar problems. Evolution is an optimization
process1. One of the major principles of evolution is heredity. Each
generation inherits the evolutionary characteristics of the previous generation
and passes those same characteristics to the next generation. These
characteristics include those of progress, growth and development. This passing
of the characteristics from generation to generation is facilitated through
genes. Since the mid 1960s, a set of new
analytical tools for intelligent optimization have surfaced that are inspired
by the Darwinian evolution theory. The
term “evolutionary computing” has been used as an umbrella for many of these
tools. Evolutionary computing comprises of evolutionary programming, genetic
algorithms, evolution strategies, and evolution programs, among others. To many
people, these tools (and names) look similar and their names are associated
with the same meaning. However, these names carry quite distinct meanings to
the scientists deeply involved in this area of research. Evolutionary programming, introduced by John
Koza2, is mainly concerned with solveing complex problems by
evolving sophisticated computer programs from simple, task-specific computer
programs. Genetic algorithms are the subject of this article and will be
discussed in detail in the next section. In evolution strategies3,
the components of a trial solution are viewed as behavioral traits of an
individual, not as genes along a chromosome, as implemented in genetic
algorithms. Evolution programs4 combine genetic algorithms with
specific data structures to achieve its goals. GENETIC
ALGORITHMS
Darwin’s theory of survival of the
fittest (presented in his 1859 paper titled On
the Origin of Species by Means of Natural Selection), coupled with the
selectionism of Weismann and the genetics of Mendel, have formed the
universally accepted set of arguments known as the evolution theory3. In
nature, the evolutionary process occurs when the following four conditions are
satisfied2: ·
An entity has the
ability to reproduce. ·
There is a
population of such self-reproducing entities. ·
There is some
variety among the self-reproducing entities. ·
This variety is
associated with some difference in ability to survive in the environment. In nature, organisms evolve as they
adapt to dynamic environments. The “fitness” of an organism is defined by the
degree of its adaptation to its environment. The organism’s fitness determines
how long it will live and how much of a chance it has to pass on its genes to
the next generation. In biological evolution, only the winners survive to
continue the evolutionary process. It is assumed that if the organism lives by
adapting to its environment, it must be doing something right. The
characteristics of the organisms are coded in their genes, and they pass their
genes to their offspring through the process of heredity. The fitter an
individual, the higher is its chance to survive and hence reproduce. Intelligence and evolution are
intimately connected. Intelligence has been defined as the capability of a
system to adapt its behavior to meet goals in a range of environments3.
By imitating the evolution process using computer instructions and algorithms,
researchers try to mimic the intelligence associated with the problem solving
capabilities of the evolution process. As in real life, this type of continuous
adaptation creates very robust organisms. The whole process continues through
many "generations", with the best genes being handed down to future
generations. The result is typically a very good solution to the problem. In
computer simulation of the evolution process, genetic operators achieve the
passing on of the genes from generation to generation. These operators
(crossover, inversion, and mutation) are the primary tools for spawning a new
generation of individuals from the fit individuals of the current population.
By continually cycling these operators, we have a surprisingly powerful search
engine. This inherently preserves the critical balance needed with an intelligent
search: the balance between exploitation (taking advantage of information
already obtained) and exploration (searching new areas). Although simplistic from a biologist's
viewpoint, these algorithms are sufficiently complex to provide robust and
powerful search mechanisms. MECHANISM OF A
GENETIC ALGORITHM The
process of genetic optimization can be divided into the following steps: 1. Generation of the initial population. 2. Evaluation of the fitness of each
individual in the population. 3. Ranking of individuals based on their
fitness. 4. Selecting those individuals to produce
the next generation based on their fitness. 5. Using genetic operations, such as
crossover, inversion and mutation, to generate a new population. 6. Continue the process by going back to
step 2 until the problem’s objectives are satisfied. The initial population is usually
generated using a random process covering the entire problem space. This will
ensure a wide variety in the gene pool. Each problem is encoded in the form of
a chromosome. Each chromosome is collection of a set of genes. Each gene
represents a parameter in the problem. In classical genetic algorithms, a
string of 0s and 1s or a bit string represents each gene (parameter).
Therefore, a chromosome is a long bit string that includes all the genes
(parameters) for an individual. Figure 1 shows a typical chromosome as an
individual in a population that has five genes. Obviously, this chromosome is
for a problem that has been coded to find the optimum solution using five
parameters.
The fitness of each individual is
determined using a fitness function. The goal of optimization is usually to
find a minimum or a maximum. Examples of this include the minimization of error
for a problem that must converge to a target value or the maximization of the
profit in a financial portfolio. Once the fitness of each individual in the
population is evaluated, all the individuals will be ranked. After the ranking,
it is time for selection of the parents that will produce the next generation
of individuals. The selection process assigns a higher probability of
reproduction to the highest-ranking individual, and the reproduction
probability is reduced with a reduction in ranking. After the selection process is
complete, genetic operators such as crossover, inversion and mutation are
incorporated to generate a new population. The evolutionary process of survival
of the fittest takes place in the selection and reproduction stage. The higher
the ranking of an individual, the higher the chance for it to reproduce and
pass on its gene to the next generation.
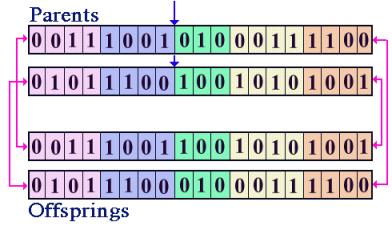
Figure 2. Simple crossover operator. In crossover, the two parent
individuals are first selected and then a break location in the chromosome is
randomly identified. Both parents will break at that location and the halves
switch places. This process produces two new individuals from the parents. One
pair of parents may break in more than one location at different times to
produce more than one pair of offspring. Figure 2 demonstrates the simple
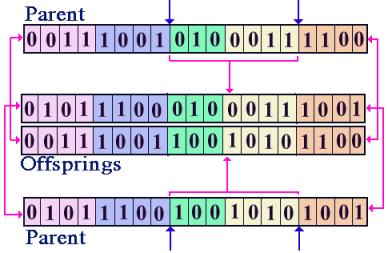
crossover. There is other crossover schemes
besides simple crossover, such as double crossover and random crossover. In
double crossover, each parent breaks in two locations, and the sections are
swapped. During a random crossover, parents may break in several locations.
Figure 3 demonstrates a double crossover process.
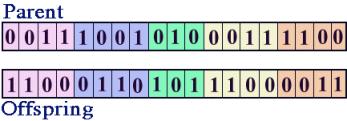
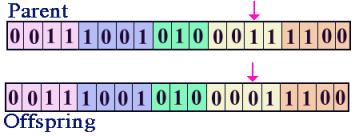
Figure 3. Double crossover operator. As was mentioned earlier, there are two
other genetic operators in addition to crossover. These are inversion and
mutation. In both of these operators the offspring is reproduced from one
parent rather than a pair of parents. The inversion operator changes all the 0s
to 1s and all the 1s to 0s from the parent to make the offspring. The mutation
operator chooses a random location in the bit string and changes that
particular bit. The probability for
inversion and mutation is usually lower than the probability for crossover.
Figures 4 and 5 demonstrate inversion and mutation. Figure 4. Inversion operator.
Once the new generation has been
completed, the evaluation process using the fitness function is repeated and
the steps in the aforementioned outline are followed. During each generation,
the top ranking individual is saved as the optimum solution to the problem.
Each time a new and better individual is evolved, it becomes the optimum
solution. The convergence of the process can be evaluated using several
criteria. If the objective is to minimize an error, then the convergence criteria
can be the amount of error that the problem can tolerate. As another criterion,
convergence can take place when a new and better individual is not evolved
within four to five generations. Total fitness of each generation has also been
used as a convergence criterion. Total fitness of each generation can be
calculated (as a sum) and the operation can stop if that value does not improve
in several generations. Many applications simply use a certain number of
generations as the convergence criterion. As you may have noticed, the above
procedure is called the classic genetic algorithms. Many variations of this
algorithm exist. For example, there are classes of problems that would respond
better to genetic optimization if a data structure other than bit strings were
used. Once the data structure that best fits the problem is identified, it is
important to modify the genetic operators such that they accommodate the data
structure. The genetic operators serve specific purposes – making sure that the
offspring is a combination of parents in order to satisfy the principles of
heredity – which should not be undermined when the data structure is altered. Another important issue is introduction
of constraints to the algorithm. In most cases, certain constraints must be
encoded in the process so that the generated individuals are “legal”. Legality
of an individual is defined as its compliance with the problem constraints. For
example in a genetic algorithm that was developed for the design of new cars,
basic criteria, including the fact that all four tires must be on the ground,
had to be met in order for the design to be considered legal. Although this
seems to be quite trivial, it is the kind of knowledge that needs to be coded
into the algorithm as constraints in order for the process to function as
expected. APPLICATION IN THE PETROLEUM INDUSTRY
There have been several applications of
genetic algorithms in the petroleum and natural gas industry. The first
application in the literature goes back to one of Holland’s students named
David Goldberg. He applied a genetic algorithm to find the optimum design for
gas transmission lines5. Since then, genetic algorithms have been
used in several other petroleum applications. These include reservoir
characterization6 and modeling7, distribution of gas-lift
injection8, petrophysics9 and petroleum geology10,
well test analysis11, and hydraulic fracturing design12-14. As it was mentioned earlier, virtual
intelligence techniques perform best when used to complement each other. The
first hybrid neural network/genetic algorithm application in the oil and gas
industry was used to design optimum hydraulic fractures in a gas storage field12-13.
A brief review of the hybrid neural network/genetic algorithm is presented
here. Virtual intelligence techniques were
utilized to design optimum hydraulic fractures for the Clinton Sand in
Northeast Ohio. In order to maintain and/or enhance deliverability of gas
storage wells in the Clinton Sand, an annual restimulation program has been in
place since the late sixties. The program calls for as many as twenty hydraulic
fractures and refractures per year. Several wells have been refractured three
to four times, while there are wells that have only been fractured once in the
past thirty years. Although the formation lacks detailed reservoir engineering
data, there is wealth of relevant information that can be found in the well
files. Lack of engineering data for hydraulic fracture design and evaluation
had, therefore, made use of 2D or 3D hydraulic fracture simulators
impractical. As a result, prior designs
of hydraulic fractures had been reduced to guesswork. In some cases, the
designs were dependent on engineers’ intuition about the formation and its
potential response to different treatments – knowledge gained only through many
years of experience with this particular field. The data set used in this study
was collected using well files that included the design of the hydraulic
fractures. The following parameters were extracted from the well files for each
hydraulic fracture treatment: the year the well was drilled, total number of
fractures performed on the well, number of years since the last fracture,
fracture fluid, amount of fluid, amount of sand used as proppant, sand
concentration, acid volume, nitrogen volume, average pumping rate, and the
service company performing the job. The match up between hydraulic fracture
design parameters and the available post fracture deliverability data produces
a data set with approximately 560 records. The first step in this study was to
develop a set of neural network models of the hydraulic fracturing process in
the Clinton Sand. These models were capable of predicting post fracture
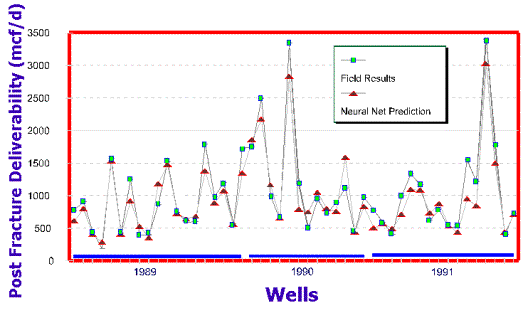
deliverability given the input data mentioned above. Figure 6 shows the neural
model’s predictions compared to actual field results for three years. Data from
these years were not used in the training process.
Once the neural network model’s accuracy was
established, it was used as the fitness function for the genetic algorithm
process to form the hybrid intelligent system. The input data to the neural
network can be divided into three categories: ·
Basic well
information ·
Well production
history ·
Hydraulic fracture
design parameters such as sand concentration, rate of injection, sand mesh
size, fluid type, etc. From the above categories, only the third (hydraulic fracture design parameters)
are among the controllable parameters. In other words, these are the parameters
that can be modified for each well to achieve a better hydraulic fracture
design. A two-stage process was developed to produce the optimum hydraulic
fracture design for each well in the Clinton Sand. The optimum hydraulic
fracture design is defined as the design that results in the highest possible
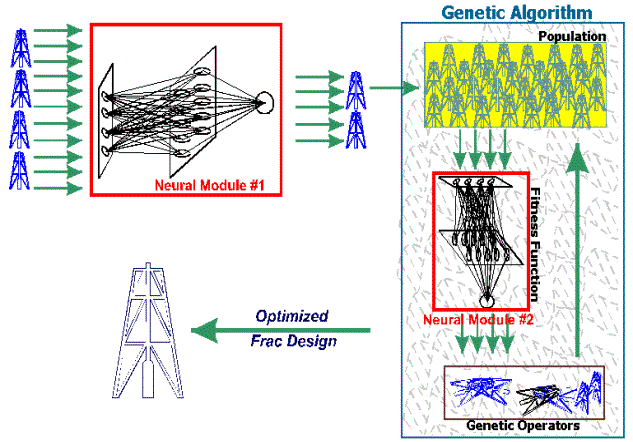
post fracture deliverability. Figure 7 is a schematic diagram of the hybrid
neuro-genetic procedure. The
neural network for the first stage (neural module #1) is designed and trained
to perform a rapid screening of the wells. This network is designed to identify
the so-called “dog wells” that would not be enhanced considerably even after a
frac job. This way the genetic optimization can be concentrated on the wells
that have a realistic chance of deliverability enhancement. The second stage of
the process is the genetic optimization routine. This stage is performed on one
well at a time. The objective of this stage is to search among all the possible
combinations of design parameters and identify the combination of the hydraulic
fracture parameters for a specific well that results in the highest incremental
post fracture deliverability. This second stage
process (the genetic optimization routine) starts by generating 100 random
solutions. Each solution is defined as a combination of hydraulic fracture
design parameters. These solutions are then combined with other information
available from the well and presented to the fitness function (neural network).
The result from this process is the post fracture deliverability for each
solution. The solutions are then ranked based on the highest incremental
enhancement of the post fracture deliverability. The highest-ranking
individuals are identified, and the selection for reproduction of the next generation
is made. Genetic operations such as crossover, inversion and mutations are
performed, and a new generation of solutions is generated. This process is
continued until a convergence criterion is reached. This process is
repeated for all the wells. The wells with highest potential for post fracture
deliverability enhancement are selected as the candidate wells. The combination
of the design parameters identified for each well is also provided to the
operator to be used as the guideline for achieving the well’s potential. This
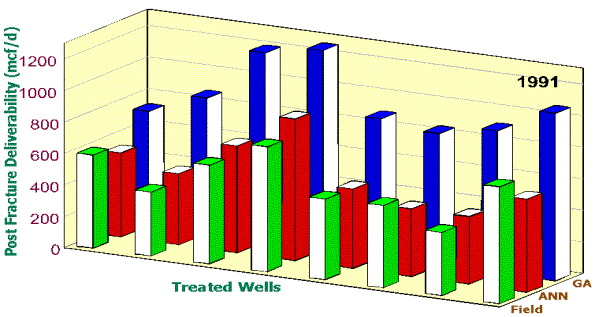
process was performed for the wells in Figure 6. The result of the genetic
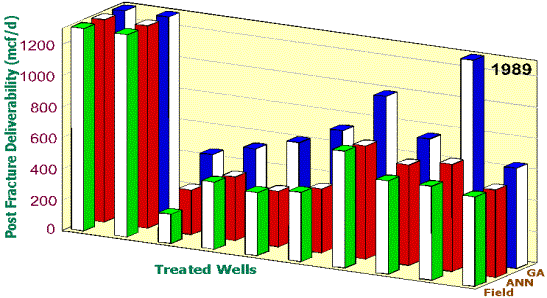
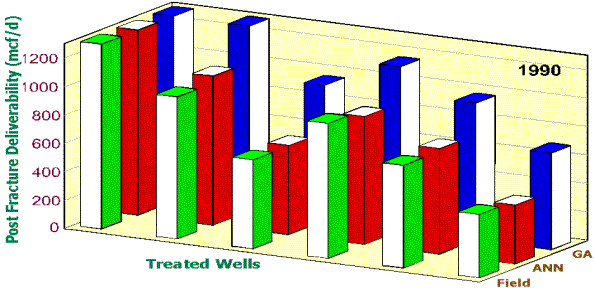
optimization is presented in Figures 8, 9, and 10. Since the same neural
networks have generated all the post fracture deliverabilities, it is expected
that the post fracture deliverabilities achieved after genetic optimization
have the same degree of accuracy as those that were predicted for each well’s
field result. In these figures, the green bars show the actual PFD of the wells
achieved in the field. The red bars show the accuracy of the neural network
used as the fitness function in the genetic optimization routine when it is
predicting the PDF, given the design parameters used in the field. The blue
bars show the PDF resulting from the same neural network that produced the red
bars, but with the input design parameters the genetic algorithms proposed.
Figure 8. Enhancement in PFD if this methodology
had been used in 1989. Please note that
the process indicates that some wells can not be enhanced, regardless of the
modification in the fracture design, while other wells can be enhanced
significantly. This finding can have important financial impact on the
operation and can help the management make better decisions in allocation of
investment.
Figure 9. Enhancement in PFD if this methodology
had been used in 1990.
Figure 10. Enhancement in PFD if this methodology
had been used in 1991. In another application,
genetic algorithms were used in combination with neural networks to develop an
expert hydraulic fracture designer14. The intelligent system
developed for this purpose is capable of designing hydraulic fractures in
detail, providing the pumping schedule in several stages (or in a ramp scheme),
and identifying the fluid type and amount, proppant type and concentration, and
the pumping rate. It was shown that fracture designs proposed by this
intelligent system are comparable to those designed by expert engineers with
several years of experience. CLOSING REMARKS Evolutionary
computing paradigms provide a rich and capable environment to solve many
search, optimization, and design problems. The larger the space of the possible
solutions, the more effective the use of these paradigms. Evolutionary
computing, in general, and genetic algorithms, specifically, are able to
combine the exploration characteristics of an effective search algorithm with a
remarkable ability of preserving and exploiting the knowledge acquired during
every step of the search as a guide to take the next step. This provides an
intelligent approach to more efficiently solve search, optimization, and design
problems. The domain
expertise is a necessity in generating useful tools using evolutionary
computing. Domain expertise must be combined with a fundamental understanding
of intelligent systems and experience in applying them in real life problems.
This will produce intelligent tools that industry can use to help its bottom
line. EFERENCES
1.
Mayr, E., Toward a new Philosophy of Biology:
Observations of an Evolutionist, Belknap Press, Cambridge, Massachusetts.
1988. 2.
Koza, J. R., Genetic Programming, On the Programming of
Computers by Means of Natural Selection, MIT Press, Cambridge,
Massachusetts. 1992. 3.
Fogel, D. B., Evolutionary Computation, Toward a New
Philosophy of Machine Intelligence, IEEE Press, Piscataway, New Jersey,
1995. 4.
Michalewicz, Z., Genetic Algorithms + Data Structure =
Evolution Programs, Springer - Verlag, New York, New York. 1992. 5.
Goldberg, D. E., Computer Aided Gas Pipeline Operation Using
Genetic Algorithms and Rule Learning, Ph.D. dissertation, University of
Michigan, Ann Arbor, Michigan. 1983. 6.
Guerreiro, J.N.C.,
et. al., Identification of Reservoir Heterogeneities Using Tracer Breakthrough
Profiles and Genetic Algorithms, SPE 39066, Latin American and Caribbean
Petroleum Engineering Conference and Exhibition held in Rio de Janeiro, Brazil,
30 August-3 September, 1997 7.
Sen, M.K. et. al.,
Stochastic Reservoir Modeling Using Simulated Annealing and Genetic Algorithm,
SPE 24754, SPE 67th Annual Technical Conference and Exhibition of the Society
of Petroleum Engineers held in Washington, DC, October 4-7, 1992. 8.
Martinez, E.R. et.
al., Application of Genetic Algorithm on the Distribution of Gas-Lift
Injection, SPE 26993, SPE 69th Annual Technical Conference and Exhibition held
in New Orleans, LA, U.S.A., 25-28 September, 1994. 9.
Fang, J.H., et. al.
Genetic Algorithm and Its Application to Petrophysics, SPE 26208, UNSOLICITED,
1992. 10.
Hu, L. Y., et.
al., Random Genetic Simulation of the
Internal Geometry of Deltaic Sandstone Bodies, SPE 24714, SPE 67th Annual
Technical Conference and Exhibition of the Society of Petroleum Engineers held
in Washington, DC, October 4-7, 1992. 11.
Yin, Hongjun, Zhai,
Yunfang, An Optimum Method of
Early-Time Well Test Analysis -- Genetic Algorithm, SPE 50905, International
Oil & Gas Conference and Exhibition in China held in Beijing, China, 2-6
November, 1998 12.
Mohaghegh, S.,
Balan, B., Ameri, S., and McVey, D.S., A Hybrid, Neuro-Genetic Approach to
Hydraulic Fracture Treatment Design and Optimization, SPE 36602, SPE Annual
Technical Conference and Exhibition held in Denver, Colorado, 6-9 October,
1996. 13.
Mohaghegh, S.,
Platon, V., and Ameri, S., Candidate Selection for Stimulation of Gas Storage
Wells Using Available Data With Neural Networks and Genetic Algorithms, SPE
51080, SPE Eastern Regional Meeting held in Pittsburgh, PA, 9-11 November,
1988. 14.
Mohaghegh, S., Popa,
A. S. and Ameri, S.: "Intelligent Systems Can Design Optimum Fracturing
Jobs", SPE 57433, Proceedings,
1999 SPE Eastern Regional Conference and Exhibition, October 21-22, Charleston,
West Virginia. A summary of this article appeared in the October 1999 issue of
JPT page 30. |
||||||||||||||||||||||