|
Distinguished Author Series VIRTUAL INTELLIGENCE
AND ITS APPLICATIONS IN PETROLEUM ENGINEERING Part 3. Fuzzy Logic Shahab Mohaghegh In two previous articles, a general overview of artificial neural networks and evolutionary computing and their applications in the oil and gas industry was presented. Fuzzy logic is the focus of this article. An overview of the subject is provided followed by its potential application in solving petroleum engineering related problems. As it was mentioned in the previous articles, the most successful applications of intelligent systems, especially when solving engineering problems, have been achieved by using different intelligent tools in concert and as a hybrid system. In this article, application of fuzzy logic for restimulation candidate selection in a tight gas formation in the Rocky Mountains will be reviewed. This particular application was chosen because it uses fuzzy logic in a hybrid manner integrated with neural networks and genetic algorithms. BACKGROUND The science of today is based on Aristotle’s crisp logic formed more than two thousand years ago. The Aristotelian logic looks at the world in a bivalent manner, such as black and white, yes and no, and 0 and 1. Development of the set theory in the late 19th century by German mathematician George Cantor that was based on the Aristotle’s bivalent logic made this logic accessible to modern science. Then, the subsequent superimposition of probability theory made the bivalent logic reasonable and workable. Cantor’s theory defines sets as a collection of definite, distinguishable objects. Figure 1 is a simple example of Cantor’s set theory and its most common operations such as complement, intersection and union.
Figure 1. Operations of conventional crisp sets. First work on vagueness dates back to the first decade of 1900, when American philosopher Charles Sanders Peirce noted that “vagueness is no more to be done away with in the world of logic than friction in mechanics1.” In the early 1920s, Polish mathematician and logician Jan Lukasiewicz came up with three-valued logic and talked about many-valued or mulivalued logic2. In 1937, quantum philosopher Max Black published a paper on vague sets3. These scientists built the foundation upon which fuzzy logic was later developed. Lotfi A. Zadeh is known to be the
father of fuzzy logic. In 1965, while he was the chair of the electrical
engineering department at UC Berkeley, he published his landmark paper “Fuzzy
Sets.4” Zadeh developed many key concepts including the membership
values and provided a comprehensive framework to apply the theory to many
engineering and scientific problems. This framework included the classical
operations for fuzzy sets, which comprises all the mathematical tools necessary
to apply the fuzzy set theory to real world problems. Zadeh used the term
“fuzzy” for the first time, and with that he provoked many oppositions. He
became a tireless spokesperson for the field. He was often harshly criticized.
For example, professor R. E. Kalman said in a 1972 conference in Bordeaux,
“Fuzzification is a kind of scientific permissiveness; it tends to result in
socially appealing slogans unaccompanied by the discipline of hard scientific
work7.” (It should be noted that Kalman is a former student of
Zadeh’s and the inventor of famous Kalman filter, a major statistical tool in
electrical engineering. Kalman filter is the technology behind the Patriot
missiles used in the Gulf War to shoot down Iraqi SCUD missiles. There has been
claims that it has been proven that use of fuzzy logic can increase the
accuracy of the Patriot missiles considerably.5-6) Despite all the
adversities fuzzy logic continued to flourish and has become a major force
behind many advances in intelligent systems.
The term “fuzzy” carries a negative
connotation in the western culture. The term “fuzzy logic” seems to both
misdirect the attention and to celebrate mental fog8. On the other
hand, eastern culture embraces the concept of coexistence of contradictions as
it appears in the Yin-Yang symbol. While Aristotelian logic preaches A or
Not-A, Buddhism is all about A and Not-A.
|
|  Figure 2. The Yin-Yang symbol. Many believe that the tolerance of eastern culture for such ideas was the main reason behind the success of fuzzy logic in Japan. While fuzzy logic was being attacked in the United States, Japanese industries were busy building a multi-billion dollar industry around it. Today, Japanese hold more than 2000 fuzzy related patents. They have used the fuzzy technology to build intelligent household appliances such as washing machines and vacuum cleaners (Matsushita and Hitachi), rice cookers (Matsushita and Sanyo), air conditioners (Mitsubishi), and microwave ovens (Sharp, Sanyo, and Toshiba), to name a few. Matsushita used fuzzy technology to develop its digital image stabilizer for camcorders. Adaptive fuzzy systems (a hybrid with neural networks) can be found in many Japanese cars. Nissan has patented a fuzzy automatic transmission that is now very popular with many other cars such as Mitsubishi and Honda8. FUZZY SET THEORY
The human thought, reasoning, and
decision-making process is not crisp. We use vague and imprecise words to
explain our thoughts or communicate with one another. There is a contradiction
between the imprecise and vague process of human reasoning, thinking, and
decision-making and the crisp, scientific reasoning of black and white computer
algorithms and approaches. This contradiction has given rise to an impractical
approach of using computers to assist humans in the decision-making process,
which has been the main reason behind the lack of success for traditional
artificial intelligence or conventional rule-based systems, also known as
expert systems. Expert systems as a technology started in early 1950s and
remained in the research laboratories and never broke through to consumer
market.
In essence, fuzzy logic provides the means to compute with words. Using fuzzy logic, experts no longer are forced to summarize their knowledge to a language that machines or computers can understand. What traditional expert systems failed to achieve finally became reality (as mentioned above) with the use of fuzzy expert systems. Fuzzy logic comprises of fuzzy sets, which are a way of representing non-statistical uncertainty and approximate reasoning, which includes the operations used to make inferences7. Fuzzy set theory provides a means for
representing uncertainty. Uncertainty is usually either due to the random
nature of events or due to imprecision and ambiguity of information we have
about the problem we are trying to solve. In a random process, the outcome of
an event from among several possibilities is strictly the result of chance.
When the uncertainty is a product of randomness of events, probability theory
is the proper tool to use. Observations and measurements can be used to resolve
statistical or random uncertainty. For example, once a coin is tossed, no more
random or statistical uncertainty remains. Most uncertainties, especially when
dealing with complex systems, are the result of a lack of information. The kind
of uncertainty that is the outcome of the complexity of a system is the type of
uncertainty that rises from imprecision, from our inability to perform adequate
measurements, from a lack of knowledge, or from vagueness (like the fuzziness
inherent in natural language). Fuzzy set theory is a marvelous tool for
modeling the kind of uncertainty associated with vagueness, with imprecision,
and/or with a lack of information regarding a particular element of the problem
at hand9. Fuzzy logic achieves this important task through fuzzy
sets. In crisp sets, an object either belongs to a set or it does not. In fuzzy
sets, everything is a matter of degrees. Therefore, an object belongs to a set
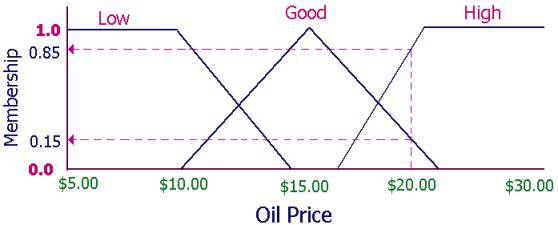
to a certain degree. For example, the price of oil today is $24.30 per barrel.
Given the price of oil in the past few years, this price seems to be high. But
what is a high price for oil? A few months ago, the price of oil was about
$10.00 per barrel. Everybody agrees that $10.00 per barrel is low. Given how
much it costs to produce a barrel of oil in the United States, one can say that
the cut-off between low and high for oil price is $15.00 per barrel. If we use
crisp sets, then $14.99 is low, and $15.01 is high. However, imagine if this
was the criterion that was used by oil company executives to make a decision.
The fact is, while $15.01 is a good price that many people will be happy with,
$16.00 is better, and $20.00 is even better. Categorizing all these prices as
high can be quite misleading. Fuzzy logic proposes the following fuzzy sets for
the price of oil.
Figure 3. Fuzzy sets representing the price of
oil. The most popular (although not yet
standard) form of representing fuzzy set and membership information is as
follows:
This representation provides the
following information: the membership m of x in fuzzy set A is m. According to the above figure, when the
price of oil is $20.00 per barrel, it has a membership of 0.15 in the fuzzy set
“Good” and a membership of 0.85 in the fuzzy set “High”. Using the above
notation to represent the oil price membership values,
Approximate Reasoning When decisions are made based on fuzzy
linguistic variables (low, good, high) using fuzzy set operators (And, Or), the
process is called the approximate reasoning. This process mimics the human
expert’s reasoning process much more realistically than the conventional expert
systems. For example, if the objective is to build a fuzzy expert system to
help us make a recommendation on enhanced recovery operations, then we can use
the oil price and the company’s proven reserves to make such a recommendation.
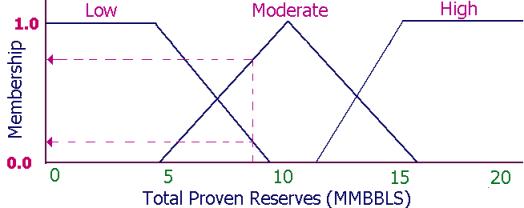
Using the fuzzy sets in Figure 3 for the oil price and the fuzzy sets in Figure
4 for the company’s total proven reserves, we try to build a fuzzy system that
can help us in making a recommendation on engaging in enhanced recovery
operations as shown in Figure 5.
Figure 4. Fuzzy sets representing the total
proven reserves.
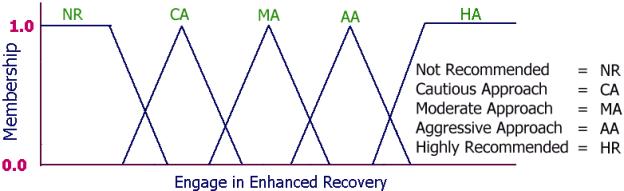
Figure 5. Fuzzy sets representing the decision
to engage in enhance recovery. The approximate reasoning is
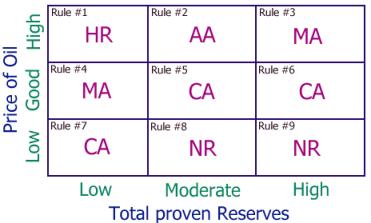
implemented through fuzzy rules. A fuzzy rule for the system being explained
here can have the following form: Rule #1: If the Price of Oil is High And the Total Proven Reserves of the company is Low
then Engaging
in Enhanced Recovery practices is Highly Recommended. Since this fuzzy system is comprised of
two variables and each of the variables consists of three fuzzy sets, the
system will include nine fuzzy rules. These rules can be set up in a matrix as
shown in Figure 6.
Figure 6. Fuzzy rules for approximate reasoning. The abbreviations that appear in the
matrix above correspond to the fuzzy sets defined in Figure 5. As one can
conclude from the above example, the number of rules in a fuzzy system
increases dramatically with addition of new variables. Adding one more variable
consisting of three fuzzy sets to the above example, increases the number of
rules from nine to 27. This is known as the “curse of dimensionality.” Fuzzy Inference A complete fuzzy system includes a
fuzzy inference engine. The fuzzy inference helps us build fuzzy relations
based on the fuzzy rules that have been defined. During a fuzzy inference
process, several fuzzy rules will be fired in parallel. The parallel rule
firing, unlike the sequential evaluation of the rules in the conventional
expert system, is much closer to the human reasoning process. Unlike in the
sequential process that some information contained in the variables may be
overlooked due to the step-wise approach, the parallel firing of the rules
allows consideration of all the information content simultaneously. There are
many different fuzzy inference methods. We will look at a popular method called
the Mamdani’s inference method10. This inference method is
demonstrated graphically in Figure 7. In this figure, a case is considered when
the price of oil is $20.00 per barrel and the company has approximately 9
MMBBLs of proven reserves. The oil price is represented by its membership in fuzzy
sets “Good” and “High”, while the total proven reserves is represented in fuzzy
sets “Low” and “Moderate”. As shown in Figure 7, this causes four rules to be
fired simultaneously. According to Figure 6 these are rules #1, #2, #4, and #5.
In each rule, the fuzzy set operation “And”, the intersection between the two
input (antecedents) variables, is evaluated as the minimum and consequently is
mapped on the corresponding output (consequent). The result of the inference is
the collection of the different fuzzy sets of the output variable as shown on
the bottom of the figure.
A crisp value may be extracted from the
result as mapped on the output fuzzy sets by defuzzifying the output. One of
the most popular defuzzification procedures is to find the center of the mass
of the shaded area in the output fuzzy sets. APPLICATION IN PETROLEUM INDUSTRY Fuzzy logic has been used in several
petroleum engineering related applications. These applications include
petrophysics11,12, reservoir characterization13, enhanced
recovery14,15, infill drilling16, decision making
analysis17, and well stimulation18-20. In this section we
review an application that incorporates fuzzy logic in a hybrid manner in
concert with neural networks and genetic algorithms. In this example of use of the intelligent systems in petroleum engineering, neural networks, genetic algorithms, and fuzzy logic are used to select candidates for restimulation in the Frontier formation in the Green River Basin20. As the first step of the methodology, neural networks are used to build a representative model of the well performance in the Frontier formation. Table 1 is a list of input parameters used in the neural network model building process.
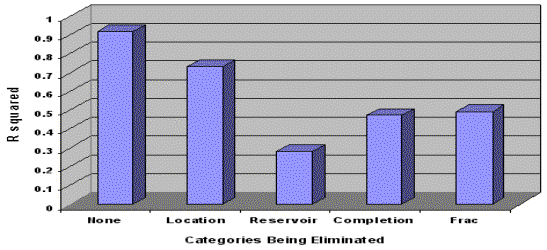
Table 1. Input parameters for the neural network analysis. Once the training, testing, and validation of the neural networks were completed, the training data set had a correlation coefficient of 0.96, and the verification data set had a correlation coefficient of 0.72. As a by-product of the neural network analysis and by using a methodology called “backward elimination,” an attempt was made to identify the most influential parameters in this data set. The results of neural network backward elimination analysis are demonstrated in Figure 8. In this figure, all four categories of the input data are shown. The most influential category has the lowest R squared. This figure shows that reservoir quality is the most important category, followed by the completion and stimulation categories that seem to be equally important. The location-related input parameters seem to be the least important parameters when compared to others. Note that among all the parameters involved in this analysis only the last three stimulation related parameters (see Table 1) are considered as being controllable.
Figure 8. Influence of parameters in the stimulation process in Frontier
formation. This brings us to the second step of the analysis that involves the genetic optimization of the stimulation parameters. In this step, the last three input parameters shown in Table 1 (namely fluid type, total fluid volume, and total proppant amount) are used in the optimization process. Using the neural network model developed in the first step of the analysis as the “fitness” function of the evolution process, the algorithm searches through all possible combinations of the aforementioned three stimulation parameters and tries to find the combination that results in the highest five-year cumulative production (5YCum). This process is repeated for every well individually. The difference between the optimized 5YCum and the actual 5YCum is considered to be the potentially missed production that may be recovered by restimulation. The outcome of this process is called the potential 5YCum and is used as one of the three inputs into step three which is the fuzzy decision support system using approximate reasoning. Step three is a three-input, one-output, fuzzy system. The
inputs include the above-mentioned potential 5YCum, a calculated parameter
called Fracs per Zone (FPZ), and pressure. The engineers in the field brought
this parameter to our attention. They mentioned that there are wells that have
been completed in all zones (there can be as many as 7 zones present) but only
one hydraulic fracture has been performed. In other words, the ratio of the
number of treatments performed to the total number zones completed is an
important factor. We also found that long-term pressure surveys had been
performed in 1995 on many wells. The issue with the pressure surveys is that
the shut-in time and the depth where the pressure readings were taken were not
consistent throughout the field. This introduces serious imprecision in the
pressure values as a comparative value from well to well. Therefore, all the
three input parameters were subjected to fuzzy sets using low, moderate, and
high fuzzy sets. The output of the fuzzy system is the degree of which a well
is a candidate for restimulation. The output fuzzy sets include: 1) the well is
a candidate, 2) the well may be a candidate, and 3) the well is not a
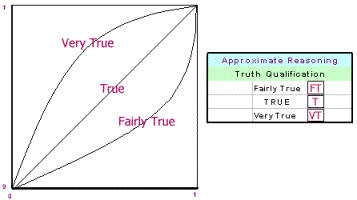
candidate. The system includes 27 fuzzy rules that are qualified using a set of
three truth functions. Figure 9 shows the 27 rules with truth qualification for
the fuzzy systems. Figure 10 shows the truth qualification Figure 9. Rules used in the fuzzy decision support system.
Figure 10. Truth qualification for the fuzzy rules. Using this three-step process, all the wells (belonging to a particular operator) in the Frontier formation was processed. A list of restimulation candidates was identified. Results It should be noted that the intelligent systems approach for this application was modified as a result of its application to three different formations, two in the Rocky Mountains and one in East Texas. The fuzzy decision support system was the most recent addition to the process. The new and improved intelligent systems approach, that included the fuzzy logic component, picked well GRB 45-12 as candidate #20, while this well was missed as a candidate prior to the addition of fuzzy logic to this procedure. An engineer with several years of experience in this field also had suggested this well as a candidate. The fuzzy decision support system was able to capture the engineer’s knowledge and use it in an automatic process for all the wells in the study. Figure 11 shows the result of restimulation on Well GRB 45-12. 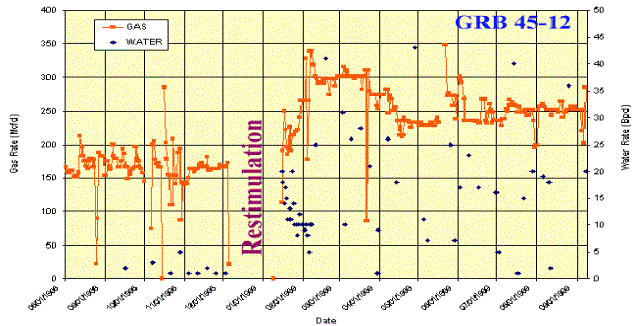 Figure 11. Gas and water production for well GRB-45-12 before and after restimulation. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||